1) MST(Minimum Spanning Tree)
신장 트리(Spanning Tree)
무방향 그래프 G(V,E)에서 E에 속한 간선들로 사이클을 포함하지 않으면서 모든 정점 V를 연결한 부분 그래프를 신장 트리(Spanning Tree)라 한다.
그래프에서 신장 트리는 여러 형태로 존재할 수 있으며, 신장 트리의 특징은 n개의 정점을 갖는 그래프에서 신장 트리에 속하는 간선의 수는 n-1개이며 사이클을 이루지 않는다는 특징이 있다.
MST란 최소 비용 신장 트리(이하 최소 신장 트리)를 뜻하며, 무방향 그래프의 간선들에 가중치가 주어진 경우, 여러 신장 트리 중에 간선들의 가중치 합이 최소인 신장 트리를 말한다.
효율적인 통신 망 설계 등에 이용될 수 있다.
2) 크루스칼(Kruskal)
크루스칼이란 위에서 말한 최소 신장 트리를 구하는 알고리즘이다.
크루스칼은 greedy하게(결정의 순간마다 최선의 결정을 함으로써 최종적인 해답에 도달) 모든 정점을 최소 비용으로 연결하여 최소 신장 트리를 구한다.
크루스칼의 핵심은 모든 간선을 가중치 기준으로 오름차순으로 정렬하고,
이 간선들을 순서대로 모든 정점이 연결될 때까지 연결하는 것이다.
Union-Find 알고리즘을 이용해서 구현할 수 있고, 이를 통해 사이클이 형성되지 않으면서 모든 정점을 연결할 수 있다.
Union-Find 알고리즘은 O(1) 즉 상수 시간 복잡도를 가지기 때문에
간선을 정렬하는 로직이 전체 시간 복잡도를 좌우하게 되는데,
가장 일반적인 퀵 정렬을 예로 들면, 퀵 정렬의 시간 복잡도인 O(ElogE)가 크루스칼 알고리즘의 시간 복잡도가 된다.
//E : 간선의 개수
//V : 정점의 개수
크루스칼 알고리즘의 동작 방식
1. 그래프의 간선들을 가중치 기준 오름차순으로 정렬한다.
2-1. 정렬된 간선 리스트를 순서대로 선택하여, 간선의 정점들을 연결한다.
2-2. 이때 정점을 연결하는 것은 Union-Find의 Union으로 구현한다.
3. 만약 간선의 두 정점 a,b가 이미 연결되어 있다면 스킵한다.
4. 위의 과정을 반복하여 최소 비용의 간선들만 이용하여 모든 정점이 연결된다.
아래에서 직접 로직을 따라가 보고, 직접 코드로 구현해보자.
3) 프림(Prim)
프림도 위에서 말한 최소 신장 트리를 구하는 알고리즘이다.
프림은 임의의 시작점에서 현재까지 연결된 정점들에서 연결되지 않은 정점들에 대해, 가장 가중치가 작은 정점을 연결하는 정점 선택 기반으로 동작한다.
프림의 핵심은 트리 집합을 단계적으로 확장하는 것이고,
새로운 정점을 연결할 때마다 새로운 정점에서 갈 수 있는 아직 연결되지 않은 정점들에 대한 간선을 추가해줘야 한다.
Priority Queue를 이용한 최소 힙으로 구현할 수 있고, 다익스트라 알고리즘과 구현 방식이 유사하다.
최소 힙으로 구현한 프림의 시간 복잡도를 구해보자.
시작점부터, 모든 정점을 탐색하는데 이 정점들은 최소 힙의 extract-min 값들이다.
따라서 모든 정점 V * extract-min에 소요되는 logV 즉 O(VlogV)이고,
정점들에서 갈 수 있는 정점들을 연결하는 간선들을 최소 힙에 추가하는 것은 최대 E번이며,
최소 힙에 최대 V개의 정점이 들어오기 때문에,
추가된 정점의 가중치를 최소 힙 내부에서 정렬하는 것은 decrease-key로 최대 logV만큼 수행된다.
따라서 모든 간선 E * 간선을 통해 삽입된 정점의 가중치 정렬 logV 즉 O(ElogV)이다.
따라서 전체 로직에 걸리는 시간은 VlogV + ElogV라고 할 수 있는데,
간선의 수는 정점의 수보다 많기 때문에 시간 복잡도에선 VlogV를 무시하여
O(ElogV)가 프림 알고리즘의 시간 복잡도가 된다.
최소 힙을 사용하지 않는 경우 O(V^2)의 시간 복잡도를 가질 수 있지만,
최소 힙으로 구현하는 것이 어렵지 않다.
또한, 피보나치 힙을 이용하는 경우 O(E + VlogV)의 시간 복잡도가 가능하지만,
대부분의 경우 최소 힙이면 충분하니 여기까지만 알아보자.
//E : 간선의 개수
//V : 정점의 개수
프림 알고리즘의 동작 방식
1. 임의의 정점을 시작점으로 선택한다.
2. 시작점에서 갈 수 있는 정점 중 가장 가중치가 작은 정점을 연결한다.
3-1. 2번 과정에서 시작점과 어떠한 정점들이 연결되었다.
3-2. 시작점과 연결된 정점들을 a집합이라 할 때, a집합에서 갈 수 있는 a집합에 속하지 않은 정점들에 대해 가중치가
가장 작은 정점을 연결한다.
4. a집합의 크기가 늘어났다.(시작점을 포함한 a집합에 새로운 정점을 연결했다.) 위의 과정을 모든 정점이 연결될
때까지 반복한다.
- kruskal.c
#include <stdio.h>
#include <stdlib.h>
#pragma region text_code
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000
int parent[MAX_VERTICES]; // 부모 노드
// 초기화
void set_init(int n)
{
for (int i = 0; i < n; i++)
parent[i] = -1;
}
// curr가 속하는 집합을 반환한다.
int set_find(int curr)
{
if (parent[curr] == -1)
return curr; // 루트
while (parent[curr] != -1) curr = parent[curr];
return curr;
}
// 두개의 원소가 속한 집합을 합친다.
void set_union(int a, int b) {
int root1 = set_find(a); // 노드 a의 루트를 찾는다.
int root2 = set_find(b); // 노드 b의 루트를 찾는다.
if (root1 != root2) // 합한다.
parent[root1] = root2;
}
struct Edge { // 간선을 나타내는 구조체
int start, end, weight;
};
typedef struct GraphType {
int n; // 간선의 개수
struct Edge edges[2 * MAX_VERTICES];
} GraphType;
// 그래프 초기화
void graph_init(GraphType* g)
{
g->n = 0;
for (int i = 0; i < 2 * MAX_VERTICES; i++) {
g->edges[i].start = 0;
g->edges[i].end = 0;
g->edges[i].weight = INF;
}
}
// 간선 삽입 연산
void insert_edge(GraphType* g, int start, int end, int w)
{
g->edges[g->n].start = start;
g->edges[g->n].end = end;
g->edges[g->n].weight = w; g->n++;
}
// qsort()에 사용되는 함수
int compare(const void* a, const void* b)
{
struct Edge* x = (struct Edge*)a;
struct Edge* y = (struct Edge*)b;
return (x->weight - y->weight);
}
#pragma endregion
// kruskal의 최소 비용 신장 트리 프로그램
// MST 그래프를 반환하도록 수정
GraphType* kruskal(GraphType* g)
{
int edge_accepted = 0; // 현재까지 선택된 간선의 수
// find 연산의 결과
// uset 선택된 간선의 start값을 Find 연산한 결과
// vset 선택된 간선의 end값을 find 연산한 결과
int uset, vset; // 정점 u와 정점 v의 집합 번호
// 선택된 간선
struct Edge e; // 그래프 포인터 선언 및 메모리 할당
GraphType* mst = (GraphType*)malloc(sizeof(GraphType));
graph_init(mst);
// 그래프 초기화
// 작은 배열을 -1로 초기화
set_init(g->n); // 집합 초기화
// 그래프 g에 속한 모든 간선을
// weight 기준 오름차순 정렬
qsort(g->edges, g->n, sizeof(struct Edge), compare);
printf("크루스칼 최소 신장 트리 알고리즘 \n");
int i = 0;
// 프로그램 버그: i<g->n 추가
while (i < g->n && edge_accepted < (g->n - 1)) // 간선의 수 < (n-1)
{
e = g->edges[i];
uset = set_find(e.start);
vset = set_find(e.end);
if (uset != vset) {
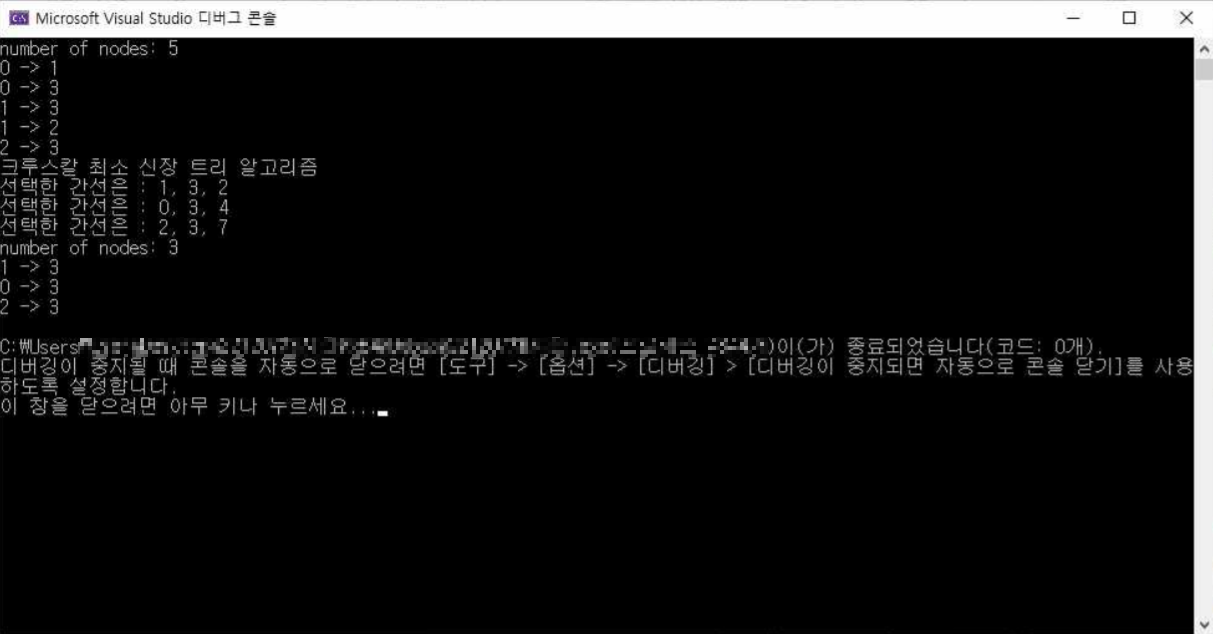
printf("선택한 간선은 : %d, %d, %d \n", e.start, e.end, e.weight);
insert_edge(mst, e.start, e.end, e.weight);
set_union(uset, vset);
}
i++;
//====================================
// 1. 선택한 간선을 g->edges[i] 로 변경
// 2. uset / vset 갱신
// set_find[index] : index 위치의 find 연산 값
// set_find[e.start] : star 위치의 find 연산 값
// 3. uset과 vset을 비교 ( 다르면 아래 내용 실행 )
// 3-1. 선택된 간선을 출력 (start, end, weight)
// 3-2. insert_edge 함수 출력
// insert_edge(mst, start, end, weight);
// 3-3 현재까지 선택된 간선의 수를 1 증가
// 3-4 uset / vset 을 union 연산
// set_union(uset, vset)
// 4. i의 값을 1 증가
//====================================
}
// mst 추가
return mst;
}
// 그래프 출력 함수
void print_graph(GraphType* g)
{
printf("number of nodes: %d\n", g->n);
for (int i = 0; i < g->n; i++) {
printf("%d -> %d\n", g->edges[i].start, g->edges[i].end);
}
}
int main(void)
{
GraphType* g, * mst;
g = (GraphType*)malloc(sizeof(GraphType));
graph_init(g);
insert_edge(g, 0, 1, 5);
insert_edge(g, 0, 3, 4);
insert_edge(g, 1, 3, 2);
insert_edge(g, 1, 2, 8);
insert_edge(g, 2, 3, 7);
// 전체 그래프 출력
print_graph(g);
mst = kruskal(g);
// mst 그래프 출력
print_graph(mst);
free(g);
free(mst);
return 0;
}- 실행결과
- prim.c
#include <stdio.h>
#include <stdlib.h>
#pragma region text_code
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000L
typedef struct GraphType {
int n; // 정점의 개수
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;
int selected[MAX_VERTICES];
int distance[MAX_VERTICES];
// 최소 dist[v] 값을 갖는 정점을 반환
int get_min_vertex(int n)
{
int v, i;
for (i = 0; i < n; i++)
if (!selected[i]) {
v = i;
break;
}
for (i = 0; i < n; i++)
if (!selected[i] && (distance[i] < distance[v])) v = i;
return (v);
}
#pragma endregion
void init_graph(GraphType* g, int n)
{
g->n = n;
for (int i = 0; i < MAX_VERTICES; i++) {
for (int j = 0; j < MAX_VERTICES; j++)
g->weight[i][j] = INF;
}
}
void build_mst(GraphType* mst, int* connected, GraphType* g)
{
for (int i = 1; i < g->n; i++) {
mst->weight[connected[i]][i] = g->weight[connected[i]][i];
}
}
GraphType* prim(GraphType* g, int s)
{
// u : 직전에 선택된 최소 distance 항목 index
// v : u와 연결된 다른 정점의 index
int i, u, v; // 최종 연결 결과물
int connected[MAX_VERTICES];
// 최종 그래프 결과물
GraphType* mst = (GraphType*)malloc(sizeof(GraphType));
init_graph(mst, g->n);
// distance 모든 초기값 INF
// selectied 모든 초기값 FALSE(0)
for (u = 0; u < g->n; u++) {
distance[u] = INF;
selected[u] = FALSE;
}
// 처음 선택된 정점의 distance 를 0으로 변경
distance[s] = 0;
// 모든 정점 개수만큼 반복
for (i = 0; i < g->n; i++) {
u = get_min_vertex(g->n);
selected[u] = TRUE;
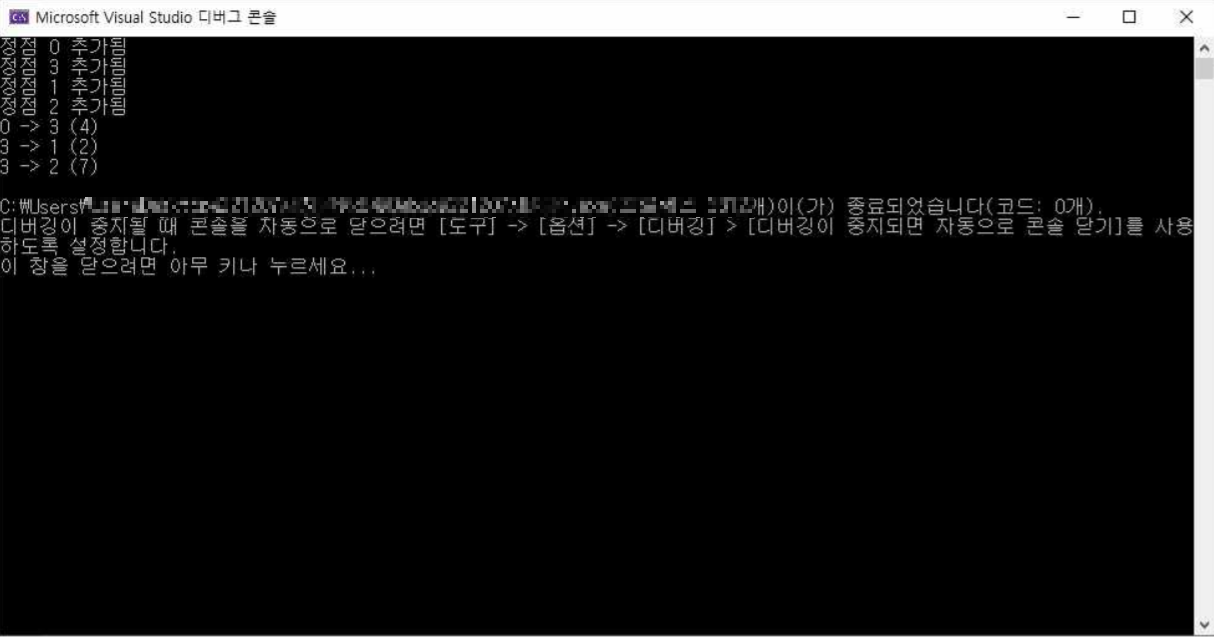
printf("정점 %d 추가됨 \n", u);
//====================================
// 1. u를 distance의 최소값으로 설정
// get_min_vertex(g->n)
// 2. 선택된 u의 selected 값을 TRUE로 변경
// 3. 선택한 정점 u 출력(ex. "정점 %d 추가됨")
//====================================
// v를 g->n 만큼 반복
for (v = 0; v < g->n; v++)
//====================================
// v에서 g로 가는 간선의 가중치가 INF가 아니고
// selected[v]가 FALSE 이면서
// (v, g) 간선 가중치 < distance[v] 라면
if (g->weight[u][v] != INF && !selected[v] && g->weight[u][v] < distance[v]) {
distance[v] = g->weight[u][v];
connected[v] = u; // 1. distance[v]를 간선의 가중치로 갱신
// g->weight[u][v]
// g->weight[v][u] 둘 다 사용 가능
// 2. connected[v]를 u로 변경
//====================================
}
}
build_mst(mst, connected, g);
return mst;
}
void print_graph(GraphType* g)
{
int i, j;
for (i = 0; i < g->n; i++) {
for (j = 0; j < g->n; j++) {
if (g->weight[i][j] != INF)
printf("%d -> %d (%d)\n", i, j, g->weight[i][j]);
}
}
}
int main(void)
{
// graph 1
/*GraphType g = { 7, {
{ 0, 29, INF, INF, INF, 10, INF },
{ 29, 0, 16, INF, INF, INF, 15 },
{ INF, 16, 0, 12, INF, INF, INF },
{ INF, INF, 12, 0, 22, INF, 18 },
{ INF, INF, INF, 22, 0, 27, 25 },
{ 10, INF, INF, INF, 27, 0, INF },
{ INF, 15, INF, 18, 25, INF, 0 } }
};*/
// graph 1
GraphType g = { 4, {
{ 0, 5, INF, 4 },
{ 5, 0, 8, 2 },
{ INF, 8, 0, 7 },
{ 4, 2, 7, 0 }}
};
GraphType* mst;
// print_graph(&g);
mst = prim(&g, 0);
print_graph(mst);
free(mst);
return 0;
}- 실행결과
'C&C++ > 자료구조' 카테고리의 다른 글
| [C/자료구조] 최대, 최소 힙(heap) 정렬 구현 (0) | 2022.11.30 |
|---|---|
| [C/자료구조] 연결 리스트 다항식 덧셈 (0) | 2022.11.20 |
| [C/자료구조] 하노이탑 문제 (0) | 2022.10.22 |
| [C/자료구조] 재귀함수를 이용한 피보나치 수열과 반복문을 이용한 피보나치 수열 (0) | 2022.10.21 |
댓글